…. tette fel a kérdést Dúl Imre matematika-fizika-informatika szakos tanárunk, majd egy cikkben ezt el is magyarázza
Reménybeli leendő matematikusunk, sajnos lassan már azt kell mondanom, hogy „volt”-tanítványom a 12.C-ből, Jaskó Martin képe a múlt matematikai segédeszközeiről: kis abakusz, hatalmas szögmérővel egybeépített favonalzó, és papír alapú tankönyvek…

Erről jutott eszembe, hogy nekem is van egy matekos relikviám valamelyik fiók mélyén, még a gimnáziumi éveimből származó logarléc. Előkerestem, az alsó és felső rész között van egy elcsúsztatható középső léc, valamint egy szintén csúsztatható leolvasó ablak, így néz ki:

A legegyszerűbb zsebszámológépek is csak a 70-es években jelentek meg nálunk, én kb. 1975-ben kaptam egyet, amit valaki az NSZK-ból hozott be, és tudta mind a négy alapműveletet! Addig mivel számoltunk, ha meg akartuk úszni a papíron való szorzásokat és osztásokat, négyzetre emeléseket és gyökvonásokat? Például a négyjegyű függvénytáblázat adataival, vagy logarléccel. Mi a működés elve? Akit érdekel, olvassa tovább! Ha pedig a történetére vagy kíváncsi, itt olvashatod el.
Az alábbi ábrából talán könnyen megérthető, hogy két sima vonalzóval hogyan lehet elvégezni pl. a 3 + 8 összeadást, ezért nem is magyarázom túl, látható, hogy 3 + 8 = 11.

Persze, nem csak ilyen egyszerű összeadásokat lehet így elvégezni, hanem bizonyos pontossággal sokkal kisebb (akár tört), vagy sokkal nagyobb számokét is. A következő kép a 3,2 + 9,3 = 12,5 összeadást szemlélteti (az egyik vonalzót megfordítottam, hogy a skálák pontosabban összeilleszthetők legyenek):

Feltételezve, hogy a diák, illetve a mérnök tisztában van a 10 hatványaival végzett műveletek szabályaival, a fenti összeadás megfeleltethető akár a 0,32 + 0, 93 = 1,25, vagy a 32 000 + 93 000 = 112.000 összeadásnak is. Kivonásra ugyanez a technika érvényes fordított lépésekkel.
A logarléc ugyanígy működik szorzásra és osztásra. Az elméleti alapot a mindannyiunk által ismert logaritmus-azonosságok teremtik meg, amely a szorzás műveletét összeadásra, az osztást pedig kivonásra vezetik vissza:
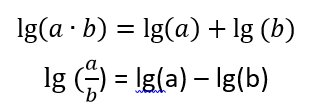
Szóval, ha a két vonalzón (lécen) nem lineáris, hanem logaritmikus skálát veszünk fel, akkor a fenti mechanizmus az összeadásból szorzást, a kivonásból pedig osztást varázsol! Nézzünk egy egyszerű példát, 2 * 4 = 8:

Természetesen, a logarléccel is lehet ennél sokkal bonyolultabb számításokat végezni, bizonyos hozzáadott tudással, korlátozott pontossággal. Azonban ez a korlátozott pontosság a legtöbb gyakorlati, akár mérnöki feladat megoldásánál is teljesen elegendő. A mai számológépeink, számítógépeink is hiába írnak ki 10 tizedesjegy pontosságú adatokat, ezeket nem vesszük figyelembe, illetve a bemeneti adatok korlátozott pontossága miatt eleve értelmetlen ilyen pontosságú eredményekre számítani.

A logarlécen az ábra szerint sok egyéb skála is van, amiről leolvasható a számok négyzete, köbe, reciproka, logaritmusa, a szögek szögfüggvényei. A léc másik oldalán egy csomó matematikai és fizikai állandó értéke kéznél van.

Összefoglalva: nagyszerű eszközt talált fel az emberiség a logarlécben. Ennek ellenére természetesen ma már én sem, és valószínűleg senki sem használja. Tudománytörténeti, technikatörténeti érdekesség.







